Justin Tzou

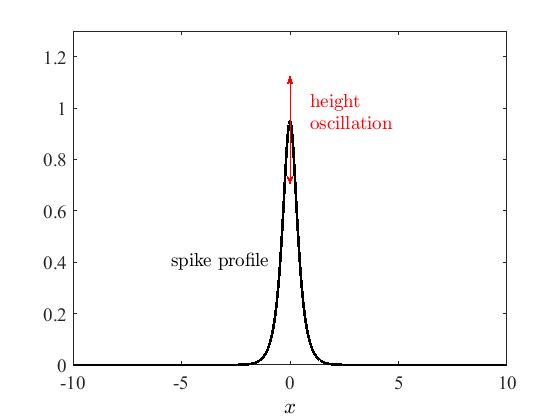
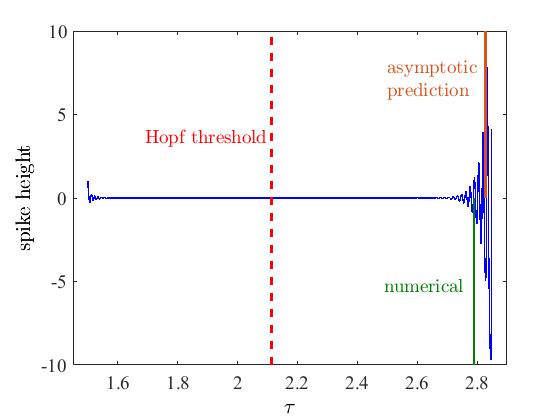
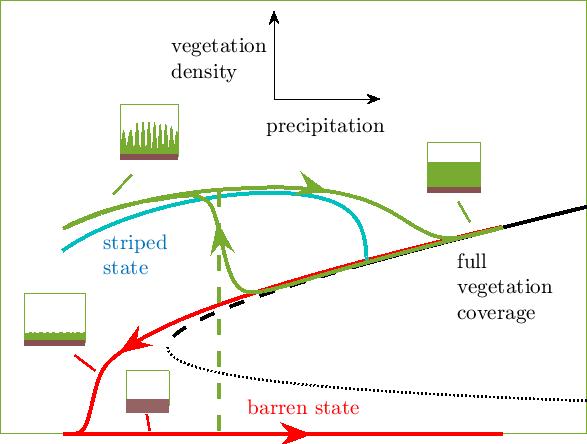
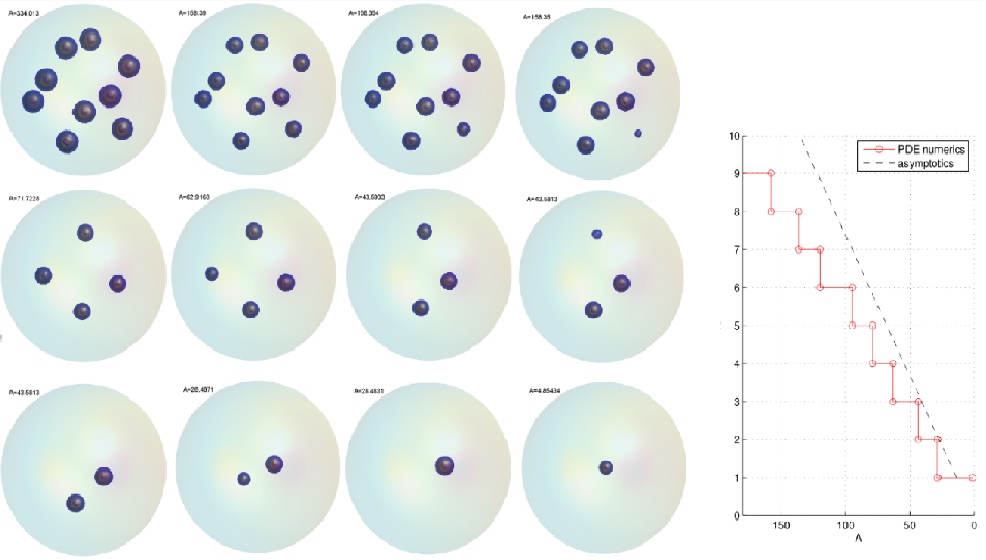
BASc, Engineering Physics, University of British Columbia, Vancouver, BC, Canada, 2007
PhD, Applied Mathematics, Northwestern University, Evanston, IL, USA, 2012
Position: Senior Lecturer, School of Mathematical and Physical Sciences, Macquarie University, Sydney, NSW, Australia
Office: E7A-12 Wally's Walk 713
Phone: +61 2 9850 8925

Email: justin dot tzou at mq dot edu dot au OR tzou dot justin at gmail dot com

CV | Research statement | Full publications list | Research highlights

Research Interests: reaction-diffusion systems; pattern formation; homoclinic snaking; singular perturbations; localized solutions; matched asymptotic methods; first passage processes and narrow escape problems; applications to vegetation patterns, cellular biology, and ecological processes
Current funding: Australian Research Council DP220101808 (co-CI with Leo Tzou, University of Sydney) Microlocal Analysis - A Unified Approach for Geometric Models in Biology; $405,000 over 3 years

Research highlights

(see here for full publications list)
The research is aimed at obtaining quantitative descriptions and critical thresholds of diffusive processes. One area of focus is mean first passage time problems in the presence of small absorbing traps (the narrow capture problem). A particular new direction of work is that in which the small traps are mobile, a scenario that arises in cellular processes and autonomous search. Challenges include not only how to derive the correct PDE for such problems, but how to solve them using asymptotic and/or numerical methods. A critical question is under which condition(s) a mobile trap becomes more effective than a stationary one. The other major area of focus is the stability and dynamics of patterns in reaction-diffusion systems in one, two, and three spatial dimensions, both near and far from the linear regime. Here, asymptotic and numerical continuation techniques are used to construct and characterize steady-state patterns. Through a combination of analytic and numerical methods, critical thresholds are obtained for various types of instabilities. The overarching themes are the techniques of analysis used (asymptotic methods, PDE techniques, numerical and continuation methods, Monte Carlo simulations), and that quantitative results yielded by the analysis often lead to rich qualitative pictures of the underlying phenomena.

1. First passage times: mobile traps, narrow capture problems, and full distributions

Consider a protein undergoing a random walk in the cytoplasm of a cell; how long on average will it take to first locate the nucleus (trap)?

quantity is referred to as the mean first passage time (MFPT)

a stationary elliptic mixed-boundary value PDE may be formulated for quantity based on a discrete random walk formalism

it is known that the nucleus does not always remain stationary; how does its motion affect the average search time?

what is the corresponding stationary PDE for this mobile trap problem?
is trap motion beneficial or detrimental to average search times?
prototype problem: consider a small circular absorbing trap of radius ε << 1 rotating with frequency ω concentric with a reflective unit disk at distance r₀ from the center
we calculate: for given ω and ε, what should r₀ be in order to optimize average search times?

Optimal radius of rotation r₀ that minimizes the average search time for each given ω. The regimes in ω are relative to the trap radius ε << 1. Further description below.
ω ~ O(1): the trap must rotate above critical frequency ω = 3.026 to be more effective than a stationary trap at the center (the trap must move fast enough in order to make up for the sampling of suboptimal search locations away from the origin)
ω >> O(1): it is optimal for the trap to rotate asymptotically close to the boundary instead of on a ``central'' ring (the trap uses the boundary to ``funnel'' the random particle into its path
ω → ∞: optimal radius of rotation is 1/√ 2 (this ``central'' ring divides the unit disk into two regions of equal area)
from paper: pdf
relevant papers: mobile trap in one dimension: pdf, multiple co-operating traps in one and two dimensions: pdf, stationary but partially absorbing trap: pdf, MFPT for random walks with centralizing drift: pdf
techniques used: regular and singular perturbation analysis, matched asymptotic methods, Green's functions, Monte Carlo simulations, finite element solutions

Often, the mean of the first passage time is not an adequate measure of the statistics of the process

e.g., when the distribution has a long and slowly decaying tail
consider a particle inside a reflective unit disk starting a random walk from (0, 0.6); what is the full distribution of times C(t) at which it will first reach a small trap centered at 0.1(cos(3π/4), sin(3π/4))?
requires solution of a 2D diffusion equation

The full distribution of capture times C(t) by a small trap of a random walker in a reflective unit disk. The particle begins its walk from (0, 0.6) while the trap is centered at 0.1(cos(3π/4), sin(3π/4)). The average capture time, averaged over all starting locations, is approximately 1.89. The full distribution is far more informative than the average.

approach: use Laplace transform to convert the time-dependent diffusion equation to a time-independent 2D elliptic problem
use matched asymptotic analysis to express solution in terms of a Helmholtz Green's function G and its regular part R
for small time (large s in Laplace domain), we can compute asymptotic solution for G and R using a boundary layer analysis
for larger time, use either a finite elements solution or a one-dimensional boundary integral solution - this method reduces a 2D time-dependent problem to a 1D time-independent problem
apply a numerical inverse Laplace transform to obtain the full distribution of capture times
short-time asymptotics can capture critical bimodal behavior:

Left panel: the random walk begins from the solid dot, while the small traps are located at the open circles. Right panel: a bimodal distribution of capture times. The first peak corresponds to capture by the single trap immediately to the right of the starting location. The second peak corresponds to capture by the five traps located farther to the left.
from paper: pdf
techniques used: boundary layer and matched asymptotic analysis, Green's functions, finite element solution, hybrid asymptotic-numerical methods, Monte Carlo simulations, Laplace transforms

2. Patterns in reaction-diffusion systems: stability, dynamics, and delayed bifurcations

When a bifurcation parameter is slowly (adiabatically) tuned from below to above a stability threshold, the full manifestation of the instability manifests well after the parameter has been tuned past threshold, resulting in a ``delayed bifurcation'' (see neuronal accommodation for a physical example)

quantitatively, this is due to a decay of the perturbation to exponentially small amplitudes while the parameter is below threshold
in a laboratory setting, this can cause an experimenter to misjudge the location of a bifurcation
a typical example is shown for a Hopf bifurcation of a single spike solution of a singularly perturbed Gierer-Meinhardt reaction-diffusion model; an explicitly solvable nonlocal eigenvalue problem (NLEP) must be analyzed to quantify the delay
the quantity being tracked is the height of the spike; as a control parameter τ is ramped slowly from below to above the Hopf bifurcation threshold (τ ~ 2.1), the height is expected to start oscillating with increasing amplitude
however, due to the delay, the oscillations are observed only well after τ has exceeded the threshold

Left panel: spatial profile of the spike. When it is unstable to an oscillatory instability, its height oscillates in time.
Right panel: the spike height (with the steady state value subtracted off) as τ is slowly ramped from below to above the Hopf bifurcation threshold (τ ~ 2.1). Notice the initial small perturbation when τ ~ 1.5. When τ < 2.1, system is stable, and so the perturbation decays. When τ > 2.1, the system is unstable, which causes the perturbation to grow. Due the the initial decay, the perturbation takes a finite amount of time to grow back to its original amplitude, during which time the control parameter has been ramped past critical. To an experimentalist, this may erroneously suggest that the bifurcation point is later than it truly is.
from paper: pdf
relevant paper: transition to a finite time blow-up of spike solutions: pdf
techniques used: matched asymptotic methods, NLEP analysis, time-dependent finite differences

The delay can also qualitatively change the outcome of a dynamical process

below, in a Klausmeier model for patterned vegetation, as the level of precipitation slowly decreases, the vegetation can either ``take refuge'' in a striped Turing state (green path), or fall off the saddle into a barren state (red path)
notice that the jump to the Turing state occurs well after the homogeneous branch loses stability
the magnitude of the delay is directly related to how much spatial noise is in the system
the outcome depends on the rate of precipitation decline versus the amount by which the Turing bifurcation is delayed - if the decline is too fast, the Turing bifurcation does not have enough time to develop, and the saddle node is activated leading to a barren state

Horizontal axis: average precipitation level; vertical axis: vegetation density. When the precipitation level decreases slowly (green curve), the full vegetation coverage state gives way to a striped vegetation state (blue branch). The jump to the Turing branch occurs well after the bifurcation point, and can be predicted asymptotically (green dashed). When the decrease is too fast (red curve), the Turing bifurcation does not have enough time to grow, and the saddle node is activated, leading to a barren state. Upon return to normal precipitation levels, the barren state persists, in contrast to the green path which allows for a return to full vegetation coverage. The asymptotic predictions are based on the rate of precipitation increase in comparison to the amount of noise in the system.
from paper: pdf
techniques used: stochastic differential equations, numerical continuation methods, time-dependent finite differences

For localized spot patterns in three dimensions, all spots are nearly identical (regardless of their location inside the bulk) due to weak inter-spot coupling caused by a fast decay of the Laplacian Green's function

a higher order analysis must be performed in order to determine how spot locations affect stability thresholds
one of the primary types of instabilities in the 3D Schnakenberg model is the ``competition'' instability, where the amount of ``fuel'' being fed into the system is insufficient to sustain the current number of spots; the linear instability leads to a nonlinear annihilation of one or more spots
below, the feed rate is being slowly decreased; the number of spots decreases as predicted by the analysis (accompanying movies)

Two-dimensional visualization of 3D spot patterns as the feed rate of the fuel is slowly decreased. Successive competition instabilities are triggered as the feed rate is decreased past certain thresholds, each leading to a nonlinear annihilation event of one of the spots. The number of spots at each given time can be predicted asymptotically (right).
the other main type of instability is referred to as a ``self-replication'' or ``peanut-splitting'' instability, which leads to a nonlinear even in which one spot splits into two
this is due to the opposite affect of the competition instability; as the feed rate is slowly increased, the system is able to support more than the current number of spots - more spots are created to consume the excess fuel (accompanying movies courtesy of Theodore Kolokolnikov)

Two-dimensional visualization of 3D spot patterns as the feed rate of the fuel is slowly increased. Successive peanut-splitting instabilities are triggered as the feed rate is increased past certain thresholds, each leading to a nonlinear self-replication event whereby one of the spots splits into two. The number of spots at each given time can be predicted asymptotically (right).
from paper: pdf
techniques used: matched asymptotic and singular perturbation methods, time-dependent finite element solutions, numerical continuation methods